I matematika může být skvělá zábava!
Pokud jste nad tímto titulkem při vzpomínce na svá školní léta nevěřícně zakroutili hlavou a řekli si: „No to tedy nemůže!“, pak je naše nová kniha VEDLE NUL JE JEDNIČKA VELKÉ ČÍSLO právě pro vás a možná vás přesvědčí, že matematika opravdu může být i zábava.
Byla  pro vás matematika ve škole učiněným hororem? Je to jediné, co jste si přes všechno vynaložené úsilí dokázali zapamatovat, trojčlenka, a to kdoví jestli? Vzpomínáte na hodiny matematiky jen jako na pachtění se se složitými vzorečky, jejichž jediný smysl podle všeho tkvěl v tom, abyste se v následujícím pololetí mohli s jejich pomocí pachtit se vzorečky ještě složitějšími, o jejichž praktické použitelnosti jste neměli ani to nejmenší ponětí? Biflovali jste se podivné poučky, u kterých se vám učitel ani nepokusil byť jen v náznacích vysvětlit, k čemu (kromě samoúčelného počítání nesmyslných příkladů v hodinách) vám u všech všudy mohou být kdy dobré?
pro vás matematika ve škole učiněným hororem? Je to jediné, co jste si přes všechno vynaložené úsilí dokázali zapamatovat, trojčlenka, a to kdoví jestli? Vzpomínáte na hodiny matematiky jen jako na pachtění se se složitými vzorečky, jejichž jediný smysl podle všeho tkvěl v tom, abyste se v následujícím pololetí mohli s jejich pomocí pachtit se vzorečky ještě složitějšími, o jejichž praktické použitelnosti jste neměli ani to nejmenší ponětí? Biflovali jste se podivné poučky, u kterých se vám učitel ani nepokusil byť jen v náznacích vysvětlit, k čemu (kromě samoúčelného počítání nesmyslných příkladů v hodinách) vám u všech všudy mohou být kdy dobré?
Matematika nemá u nás dobrou pověst a obzvlášť ve vyšších ročnících středních škol se pro mnoho žáků stane noční můrou. Německý fyzik a žurnalista Holger Dambeck ale ve své knize plné matematických triků ukazuje, že to tak být nemusí. Matematika pro něj není biflování vzorců, ale zábavné přemýšlení a nalézání geniálních řešení. Přináší tipy a fígle na první pohled vyloženě „matematické“, jako triky pro snadné násobení velkých čísel nebo dělení kruhu na pětiúhelníky, ale z matematického úhlu pohledu se dívá i na věci, u kterých by vás to možná nenapadlo, jako je vázání uzlů a kravat, kouzlení s kartami nebo sbírání samolepek.
Kniha je určená všem, kdo nad matematikou ještě nechtějí zlomit hůl - anebo nemohou, protože se s ní stále potýkají ve škole a začínají k ní pociťovat odpor. Tato kniha je možná ještě přesvědčí o tom, že matematika může být užitečná - jakkoliv je způsob výuky na našich školách často nemůže dovést k jinému závěru než přesně opačnému.
Holger Dambeck vystudoval fyziku a pracuje jako redaktor ve Spiegel Online, kde píše dva pravidelné matematické sloupky. Je nositelem ceny Německé matematické společnosti. Portál vydal i jeho úspěšnou knihu Přijdou tři logici do baru…
Ukázka:
Skládání místo rýsování: origamics
Jistě znáte japonské umění skládání papíru origami. Hvězdy, jeřáby, labutě, to vše lze vykouzlit ze zpravidla čtvercového listu papíru. Dokonce i matematici se zajímají o promyšlené skládání, protože umožňuje geometrické konstrukce, které není možné sestrojit pomocí kružítka a pravítka. Pro matematicky motivované skládání bylo dokonce vytvořeno zvláštní slovo: origamics – složenina origami a mathematics, anglického slova pro matematiku.
V závěru této kapitoly bych vám některé z těchto geometrických skládacích triků rád představil. Začněme s pravidelným pětiúhelníkem. Ten může být totiž také složen. Potřebujete k tomu pouze dlouhý úzký pruh papír. Například můžete odstřihnout 3 až 4 centimetry široký pruh z dlouhé strany listu A4. Ujistěte se také, že má konstantní šířku.
Vezměte si svůj proužek, vytvořte na jednom jeho konci smyčku a protáhněte jí druhý konec proužku. Takže vlastně na papírovém pruhu vytvoříte jednoduchý uzel. Nyní je důležitý cit v prstech: Utahujte uzel kousek po kousku. Proužek však nesmí být nikde pokrčen, musí si všude zachovat svou šířku. Při žádané pečlivosti vznikne úhel o velikosti přesně 108°, což odpovídá vnitřnímu úhlu pravidelného pětiúhelníku.
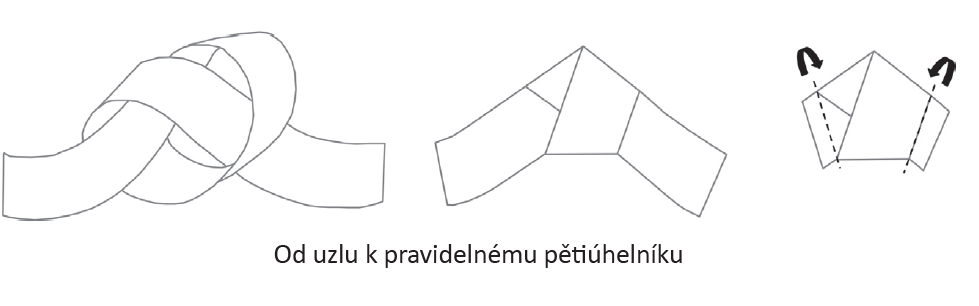 Tři strany pětiúhelníku jsou již jasně rozpoznatelné. Nyní zbývá pouze nůžkami zastřihnout oba přesahující konce papírového proužku, úhledně je založit a váš pravidelný pětiúhelník je hotov!
Tři strany pětiúhelníku jsou již jasně rozpoznatelné. Nyní zbývá pouze nůžkami zastřihnout oba přesahující konce papírového proužku, úhledně je založit a váš pravidelný pětiúhelník je hotov!
Jako matematicky zainteresovaná osoba si určitě pokládáte otázku: Je tento pětiúhelník skutečně rovnostranný? Jinými slovy jsou všechny vnitřní úhly a všechny strany stejné velikosti? Pokud chcete, můžete si to zkusit dokázat sami.
Nebo si to můžete nechat vysvětlit ode mě. Bohužel důkaz také není úplně snadný. Obrázek níže zobrazuje uzel. Vzhledem k předchozímu nákresu je však otočený o 180°. Vrcholy pětiúhelníku, o kterém nevíme, zda je rovnostranný, si označíme A, B, C, D a E.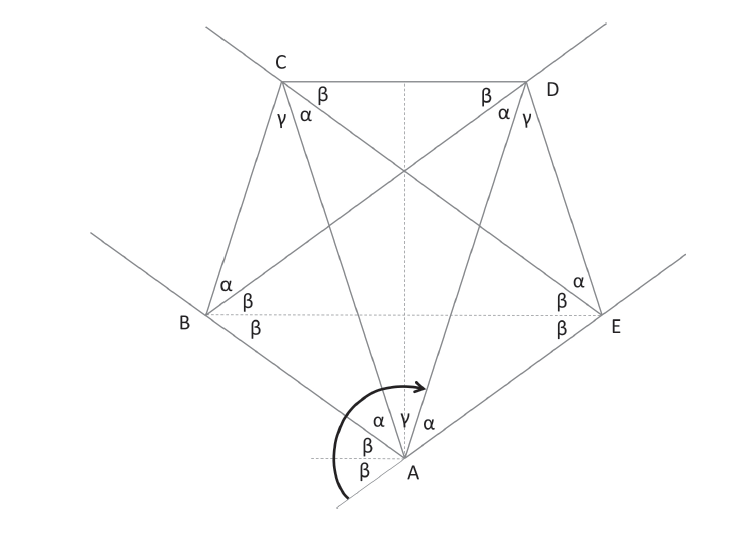
V našem pětiúhelníku je několik rovnoběžných úseček, například DE a AC. Jsou rovnoběžné, protože jsou tvořeny okraji zauzlovaného papírového pruhu. Kromě toho víme, že uzel musí být symetrický. Pokud vyměníme přední stranu za zadní, tedy uzel převrátíme, nic se na něm nezmění. Proto mu můžeme nakreslit osu symetrie, na obrázku je to čárkovaná svislá čára. Díky symetrii také víme, že úhlopříčka BE musí být rovnoběžná s CD.
Nyní označíme úhly nacházející se v pětiúhelníku a využijeme skutečnosti, že určitá přímka vždy protíná dvě navzájem rovnoběžné přímky pod stejným úhlem. Například úhly ACE a BAC jsou stejně velké, označíme je písmenem α. Kvůli symetrii mají tři úhly u vrcholů C a D, stejně jako B a E, stejné velikosti. Vidíme, že tři různé úhly α, β, γ jsou dostačující pro popsání všech 15 vnitřních úhlů. Například úhly ECD (= β) a BEC jsou shodné, protože přímka CE protíná dvě navzájem rovnoběžné úsečky CD a BE. Tedy úhel BEC = β. Analogicky odvodíme zbývající vnitřní úhly. Nyní musíme ukázat, že všechny tyto úhly mají stejnou velikost (α = β = γ) a také že strany pětiúhelníku mají stejné délky.
 Zkuste i další knihu Holgera Dambecka Přijdou tři logici do baru..., aneb sto nejhezčích logických a matematických hádanek.
Zkuste i další knihu Holgera Dambecka Přijdou tři logici do baru..., aneb sto nejhezčích logických a matematických hádanek.
Nejprve se podívejme na vnější úhel u bodu A, který má velikost 2β, protože je to střídavý úhel k úhlu DBA pro rovnoběžky BD a AE. Zde je papírový proužek přicházející z pravého horního rohu přeložen, úsečka AB je ohybová hrana. Přeložený pruh pak jde nahoru až k dalšímu skladu podle úsečky CD, poté doprava dolů ke hraně AE a odtud nakonec doleva nahoru. Přehýbání okrajů funguje stejně jako zrcadlo: Úhel dopadu je stejný jako úhel odrazu. Tedy α + γ se musí rovnat vnějšímu úhlu v bodě A. Velikost vnějšího úhlu již známe. Jelikož AB je rovnoběžná s CE, úhel je β + β. Tedy α + γ = β + β. Z toho dále vyplývá, že trojúhelníky ACE a ABD jsou rovnoramenné. Protože ACD je také rovnoramenný, jsou čtyři úhlopříčky AC, AD, BD a CE všechny stejné délky.
Nyní se podívejme na úhlopříčku AC. Papírový proužek, který přichází seshora zleva, má šířku sin (α) × AC. Po skladu proužek směřuje nahoru k CD. Jeho šířku lze vypočítat jako sin (γ) × AC. Protože šířka proužku se nemění, musí mít úhly α a γ stejnou velikost. Dostáváme tedy: α = β = γ. Z toho dále vyplývá, že úhlopříčka BE má stejnou délku jako zbývající čtyři úhlopříčky. A konečně se dostáváme k tomu, že v našem pětiúhelníku mají všechny vnitřní úhly a všechny strany stejnou velikost. Jedná se tedy opravdu o pravidelný pětiúhelník. Jsme hotovi s tímto ne úplně jednoduchým důkazem.
Trisekce úhlu
To je kvadratura kruhu! Pravděpodobně jste tuto frázi už slyšeli. A pravděpodobně také víte, odkud pochází. Dokonce už staří Řekové se marně snažili najít k danému kruhu čtverec se stejným obsahem. Ale teprve v 19. století se podařilo dokázat německému matematikovi Ferdinandu von Lindemannovi, že kvadratura kruhu není možná. Vinu na tom koneckonců nese číslo pí.
Není velmi známé, že kvadratura kruhu je problém trisekce úhlu. Rozdělení úsečky na tři stejné části pomocí kružítka a pravítka nepůsobí žádné velké potíže. Ale jak rozdělit na třetiny úhel?
Dokonce i staří Řekové to zkoušeli, ale bez úspěchu. Trvalo asi 2000 let, než nějaký matematik předložil důkaz. Pierre Laurent Wantzel (1814–1884) dokázal, že tuto úlohu kružítkem a pravítkem vyřešit nelze.
Takže pokud chcete rozdělit pizzu spravedlivě na tři kousky, nemáte jinou možnost, než sáhnout po úhloměru, vypočítat úhel a za pomoci úhloměru vyznačit řeznou linii.
Ale existuje jednoduchý trik, pomocí kterého lze dosáhnout nemožného, trisekce úhlu. Musíte list papíru, na kterém je daný úhel zakreslen, důmyslně poskládat.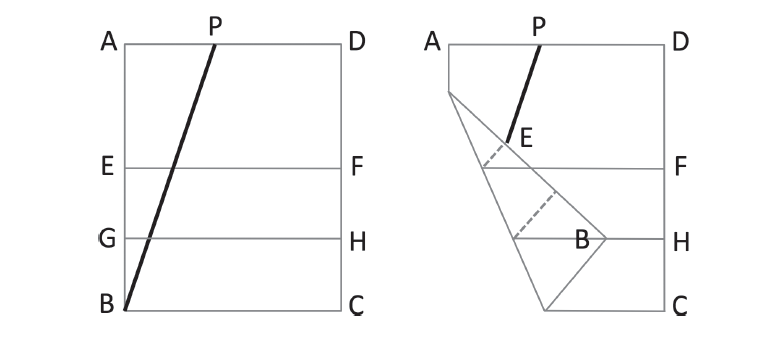 Obrázek ukazuje úhel PBC, který chceme rozdělit na tři stejně velké díly. Jeho ramena jsou tvořena úsečkami PB a BC a bod B je vrchol našeho úhlu.
Obrázek ukazuje úhel PBC, který chceme rozdělit na tři stejně velké díly. Jeho ramena jsou tvořena úsečkami PB a BC a bod B je vrchol našeho úhlu.
Body A, B, C, D označují rohy listu našeho papíru. Nejprve zakreslíme zhruba v polovině papíru vodorovnou úsečku EF. Přesně uprostřed mezi EF a BC, dolní hranou listu, narýsujeme druhou úsečku GH, rovnoběžnou s okrajem papíru.
Nyní začneme se skládáním: Uchopíme roh papíru B a posouváme ho po úsečce GH sem a tam, dokud bod E neleží na úsečce BP, horním ramenu úhlu, který chceme rozdělit na třetiny. V okamžiku, kdy body B a E leží na uvedených úsečkách, přeložíme list papíru podle obrázku. Označíme si bod, ve kterém se B dotýká úsečky GH, a pojmenujeme ho bod B’; analogicky taktéž označíme bod E’ – viz obrázek níže.
Okraj přeloženého papíru protíná GH v bodě I. Nyní jsme hotovi: úsečky BB’ a BI rozdělují náš úhel PBC na třetiny.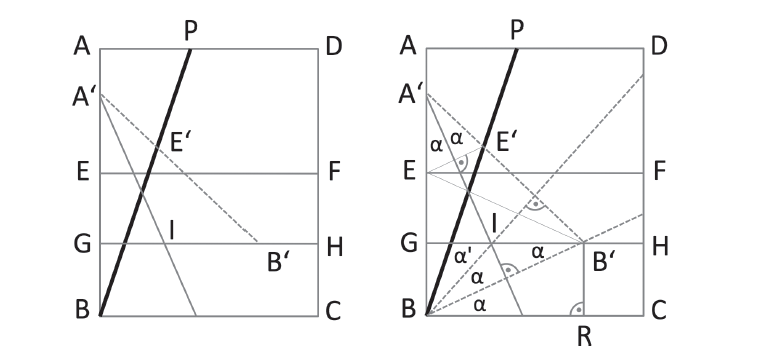 Skoro se nedá uvěřit, že tento jednoduchý skládací trik řeší problém, který matematici nemohou vyřešit za pomoci kružítka a pravítka.
Skoro se nedá uvěřit, že tento jednoduchý skládací trik řeší problém, který matematici nemohou vyřešit za pomoci kružítka a pravítka.
Ale opravdu jsme rozdělili úhel přesně na třetiny? To není příliš těžké dokázat. Když jsme přeložili papír podél úsečky A’I, vznikla nám celá řada pravých úhlů. Úsečky EE’ a BB’ jsou kolmé k hraně překladu. Začátek hrany přehybu v bodě A’ tvoří spolu s body B a B’ rovnoramenný trojúhelník. Hrana přehybu dělí úhel u horního vrcholu tohoto trojúhelníku na polovinu, oba vzniklé úhly stejné velikosti si označíme α.
Úhel CBB’ je rovněž velikosti α, protože když se podíváme na součet vnitřních úhlů levé poloviny právě zmíněného rovnoramenného trojúhelníku, zjistíme, že úhel B’BA = 9 − α. Totéž platí pro úhel BB’G a kvůli symetrii i pro úhel IBB’. Nyní nám ještě zbývá ukázat, že úhel IBE’, který si označíme α’, je také stejně velký jako α.
Prodloužení úsečky BI je kvůli přehybu, který odpovídá osové souměrnosti, kolmé na E’B’. Pokud by měly obě strany BE’ a BB’ stejnou délku, BB’E’ by byl rovnoramenný trojúhelník. Kolmice by tedy automaticky dělila úhel napůl, což by znamenalo, že α = α’.
Ve skutečnosti má BE’ opravdu stejnou délku jako BB’. Čtyři body E, E’, B, B’ tvoří lichoběžník, jehož osa symetrie je hrana přehybu. Proto mají obě jeho úhlopříčky BE’ a EB’ stejnou délku. EB’ má však přesně stejnou délku jako BB’, protože GH leží přesně uprostřed mezi EF a BC. Tedy trojúhelník BB’E’ je opravdu rovnoramenný. A tím jsme dokázali, že úsečky BI a BB’ doopravdy dělí daný úhel na třetiny.
Já jsem stále ještě ohromen, jaké dovedné kousky jsou pomocí origamics možné. Není to bláznivé, že jeden přehyb papíru udělá z problému, který není řešitelný kružítkem a pravítkem, úlohu téměř dětinsky jednoduchou?
A ještě další věc mi přijde podivuhodná: Pětiúhelníkový uzel, který je tak jednoduché vytvořit, udělá většinu matematické práce za nás. Protože dokázat, že pětiúhelníkový uzel z papíru opravdu tvoří rovnostranný pětiúhelník, není tak snadné jako důkaz trisekce úhlu pomocí přehybu.
Nezáleží na tom, zda jste zvládli sledovat komplikovanou důkazovou argumentaci, nebo ne. V každém případě jste nyní geometricky vyzbrojení, takže nemusíte mít strach z velikonočních vajec nebo z krájení pizzy.
Portál byl založen v roce 1990 s cílem pomáhat při výchově dětí a mládeže. Od začátku se proto zaměřil především na publikace z oborů pedagogika, psychologie a sociální práce, a to na odborné i populární úrovni. Později přibyly knihy pro rodiče i děti jak z oblasti beletrie, tak rozvíjející tvořivost. Nedílnou součástí knižní produkce jsou rozhovory, spirituální tituly, beletrie a non-fiction.